The “Kryptos” sculpture, dedicated in 1990 by its creator Jim Sanborn, contains four encoded messages. Cryptography enthusiasts have successfully decoded three of them. However, the elusive fourth ciphertext, K4, remains undeciphered, presenting a fascinating challenge to the global community of cryptanalysts, even 34 years after its creation.

Since 2010, Sanborn has offered clues (1, 2), hoping someone will solve them. To date, these cribs—as they are referred to within the field of cryptanalysis—are:

• The 22^nd through 34^th positions correspond to EASTNORTHEAST,

• The 64^th through 74^th positions correspond to BERLINCLOCK.

Despite these known plaintext words, K4 has yet to be deciphered. While our attempts have not yielded a solution, we have just discovered a pattern that may provide valuable insights into the encryption method employed for K4.

We first share our findings as a bottom line. Then, we detail our approach and evaluate the relevance of this pattern.

The Signs of a Segmentation and Recombination Technique

We believe that:

• The letter ‘W’ acts as a separator that splits K4 into six segments. (We define a segment as a contiguous series of characters that can be deciphered into a partial or a complete sentence, as in this fictitious example: HLMKZJZDDSABW, a ciphertext segment, corresponding to BROWNFOXJUMPS, a plaintext segment.)

• Consequently, unlike other characters, the letter ‘W’ is not mapped to plaintext characters. Additionally, despite the ciphertext’s total length of 97 characters, the plaintext can contain no more than 91 characters (97 - 6 occurrences of ‘W’).

• Each segment belongs to either of two groups (Group A and Group B).

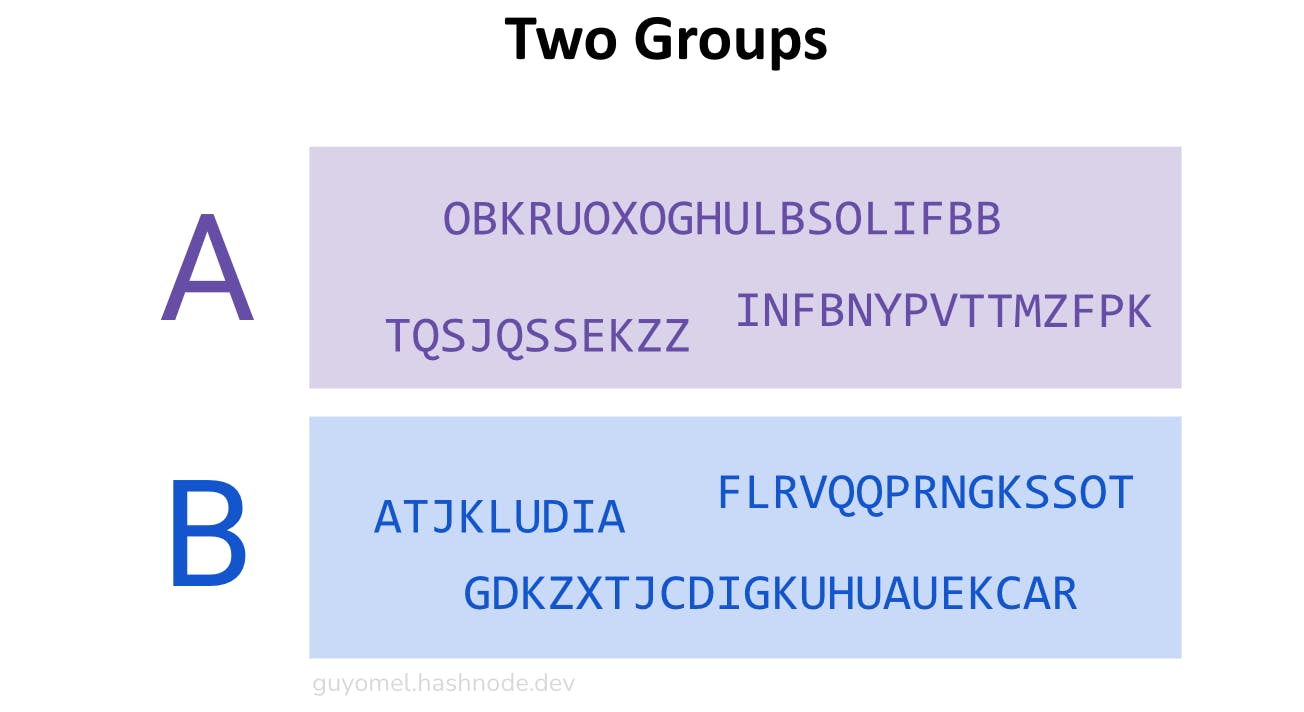
• The groups appear alternatively in the ciphertext: A|B|A|B|A|B.

• The groups have identical letter frequency distribution shapes for different letters. In each group,

  • 1 letter appears 5 times,

  • 2 letters appear 4 times each,

  • 4 letters appear 3 times each,

  • 5 letters appear 2 times each, and

  • 9 letters appear 1 time each.

Based on these findings, we assume that:

• The passage has been enciphered by a mechanism that preserves the position of the words (substitution cipher). Indeed, a transposition cipher would not be compatible with such a segmentation: the latter requires preserving the original positions.

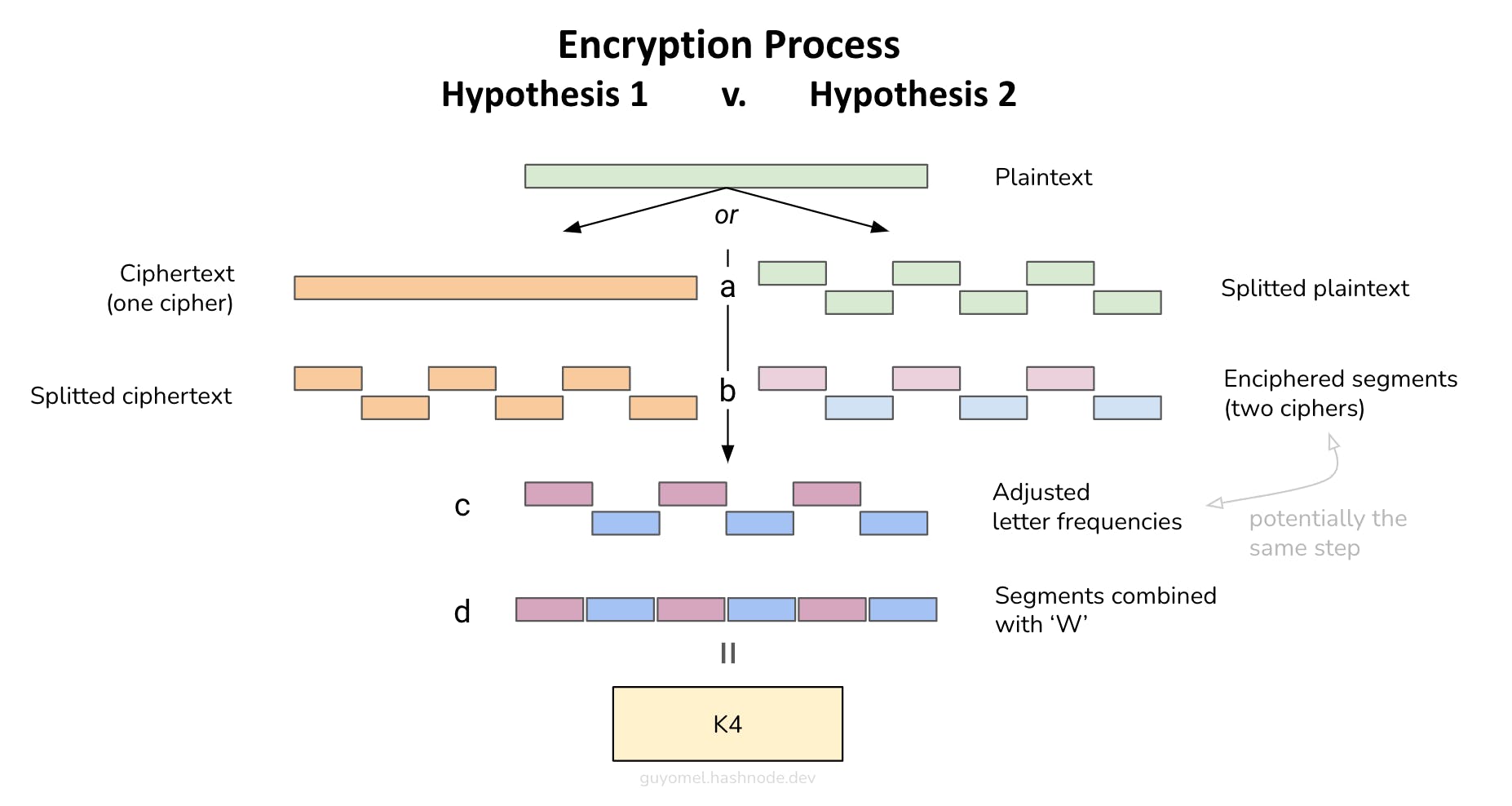
• The transformation of the plaintext into the ciphertext has been carried out using one of the following methods, both illustrating a “segmentation and recombination” technique:

  1. (Hypothesis 1) The plaintext has first been enciphered (a) and then split into segments divided into two groups (b), adjusted to have the same letter frequency distribution shapes (c), and recombined with intermediary letters ‘W’ (d),

  2. (Hypothesis 2) The plaintext has first been split into segments divided into two groups (a), then each segment has been enciphered using a technique specific to its group (b); additionally, the groups have been adjusted to have the same letter frequency distribution shapes (c), before being recombined with intermediary letters ‘W’ (d). (Note that, in that case, we do not exclude the possibility that the steps (b) and (c) could have been performed in one step).

Our Approach

While studying Enigma (hypothesizing it would help solve K4), we learned that separators represented punctuation marks as the machine only supported alphabetic characters. For instance, the doublet “YY” represented a dot. These separators were used for plaintext because of a technical constraint. We pondered if this technique could have been replicated in ciphertext to misdirect analysts.

To systematically explore this idea, we created K4nundrum.

This open-source tool splits K4 on different separators and analyzes the resulting segments. K4nundrum explores separators ranging from ‘A’ to ‘Z’ and uses them to split the ciphertext, subsequently permuting the resulting segments. Every permutation is distributed into different groups (from two groups for the whole ciphertext, up to one group per segment). Ultimately, K4nundrum examines each collection of groups to ascertain whether they exhibit identical letter distribution characteristics.

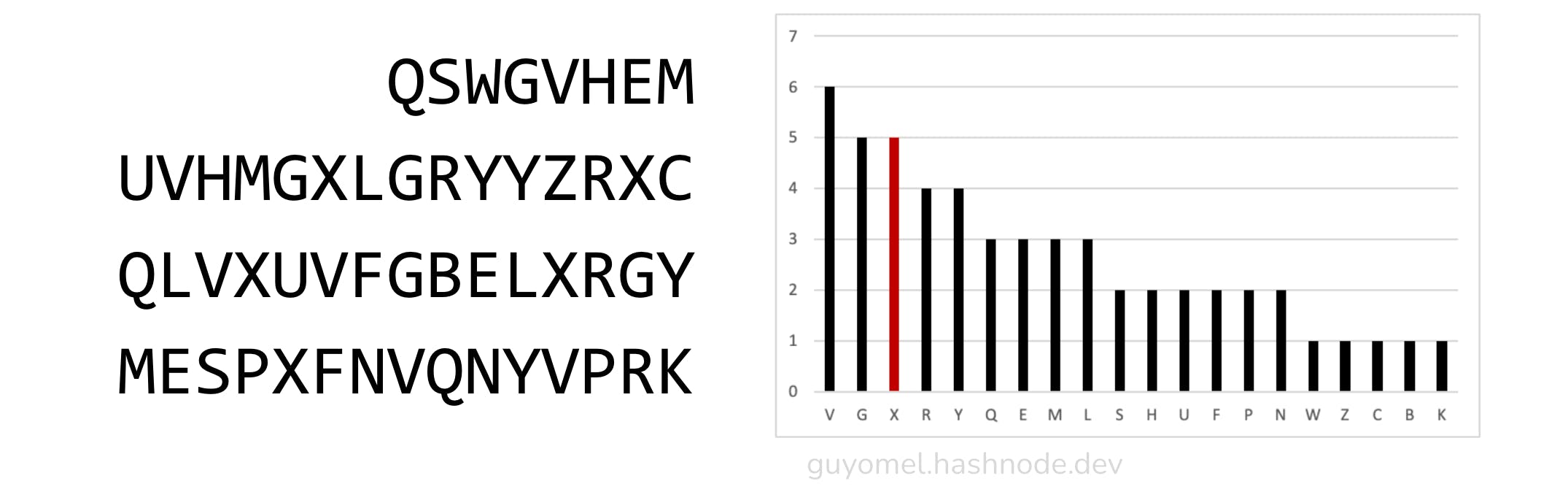
Using this process, K4nundrum unveiled that splitting K4 based on the letter ‘W’ produces groups of segments with identical letter frequency distribution shapes when permuted according to a specific arrangement (alternating groups). As mentioned above, these two groups are { INFBNYPVTTMZFPK, OBKRUOXOGHULBSOLIFBB, TQSJQSSEKZZ } and { ATJKLUDIA, FLRVQQPRNGKSSOT, GDKZXTJCDIGKUHUAUEKCAR }.

An Intentional Pattern?

This pattern is interesting: it is nonobvious, which would explain why it protected K4’s plaintext so well. At the same time, it would have been relatively easy for the creator of Kryptos to implement (we attempt to demonstrate it with an illustrative example below). But couldn’t it be just coincidental?

To understand how frequently such a pattern would occur in a string of text the length of K4, we have added a feature to K4nundrum that simulates “pseudo-K4s” (enabled with the --sim flag). These pseudo-K4s are random strings of 97 uppercase letters. (By definition, we cannot create a process that would generate perfect K4-like strings, as the underlying encryption method is unknown). While these strings are not generated like the original K4, this simulation gives a general indication of how frequently this phenomenon can be noticeable by an external observer.

Simulations empirically indicate, based on the generation of more than one million pseudo-K4s, that this pattern naturally emerges less than 2% of the time. This probability is low but does not necessarily make this hypothesis a reality. Fortunately, several indicators demonstrate that K4’s pattern has characteristics that make it less likely to occur just by chance.

First, the simulator tends to produce groups containing tiny segments (1 or 2 characters long). For instance, and typically:

> GKUCPFTQBJCKSEVMFWRLWKPEKCZHFFYNPLZZINWAFVKZEMJNRCAUYHUMITLKEZKQGZKBG
PIRRPUGKVSMHXASUIYPVJBZKFUKX

  Group 1:           BGPIRRPUG FU G PE QGZ UCPFTQBJC X ZEMJNRCAUYHUMITL
  Letter Freq.:      U:5 G:4 P:4 R:3 C:3 E:2 B:2 I:2 F:2 Z:2 M:2 J:2 
                     T:2 Q:2 H:1 L:1 X:1 N:1 Y:1 A:1

  Group 2:           CZHFFYNPLZZINWAFV EZ SEVMFWRLW VSMHXASUIYPVJBZ
  Letter Freq.:      Z:5 V:4 F:4 W:3 S:3 H:2 E:2 P:2 L:2 M:2 N:2 Y:2 
                     I:2 A:2 J:1 X:1 R:1 U:1 C:1 B:1

The random string produces segments such as ‘EZ’ or ‘G’ in this example.

If we assume that segments represent sequences of whole words, it is implausible that the creator of a ciphertext would use small segments. They would additionally needlessly add complexity to the encryption process. When the simulator excludes tiny segments (less than three characters), ~0.5% of the pseudo-K4 passages can be split into appropriately sized groups with identical distribution shapes.

Second, K4’s groups alternate. This additional constraint is even more rarely visible in the segments generated by the simulator: ~0.07% of the pseudo-K4s alternate. When all these constraints are considered (identical letter frequency distribution shapes, appropriately sized segments, and alternating groups), only ~0.05% of the generated strings are similar to K4. One way of putting it is that if we consider that this pattern happens merely by chance, on average, Sanborn would have had to create 2,000 Kryptos—each encoding a different message—so that one K4-like pattern would have been noticeable to an external observer.

Third, when we superpose the cribs with K4, the plaintext words are immediately adjacent to other segments. In other words, when mapped to the ciphertext, their first or last letter is directly next to a ‘W’: they start or end a segment. This observation could support the idea of segments representing sequences of whole words.

Suppose we assume that segments are to be deciphered to (partial) sentences with complete words (the second segment, consisting of 15 characters, could, for instance, mean “… east-northeast of …”). In that case, the probability that such a pattern would emerge just by chance becomes even lower. Speculatively, it may be significant that Jim Sanborn, anxious to see his work finally deciphered, revealed words belonging to two different groups (BERLINCLOCK belonging to Group A, and EASTNORTHEAST to Group B)—as a kind of meta-clue.

Last, and more anecdotally, a similar pattern appears in the Mengenlehreuhr, known as the “Berlin Clock”, which segmentally tells the time using colored fields. This is perhaps what Sanborn meant when he cryptically said, “You’d better delve into that particular clock”. That is, that segmented clock.

For these reasons, a coincidence, while not impossible, seems very unlikely. In other words, we are confident that this pattern is intentional.

A Technique to Mask Letter Frequencies

Fabricating Letter Frequencies

Why would Sanborn use such a technique?

First, as mentioned above, a segmenting and recombining technique conveniently produces nonobvious patterns. It is asymmetrical: it does not require a deep knowledge of cryptographic methods for its implementation; at the same time, it easily defeats classic cryptanalysis attacks by adding characters—the separators—that are not mapped to the plaintext and misleading people to think that the ciphertext must be analyzed as a whole. In the context of K4, this is all the truer because the passage is so brief.

Second, this technique can mask the letter frequency by combining multiple letter frequencies. Let’s take ‘K’ for example. It appears eight times in the original K4. By analyzing it under the lens of the segmentation technique, these occurrences result from combining three occurrences in Group A and five in Group B. By adjusting the letter frequency of one (or both) of the groups, it becomes possible to fabricate a new letter frequency distribution. Additionally, the letter separator pollutes the letter frequency distribution.

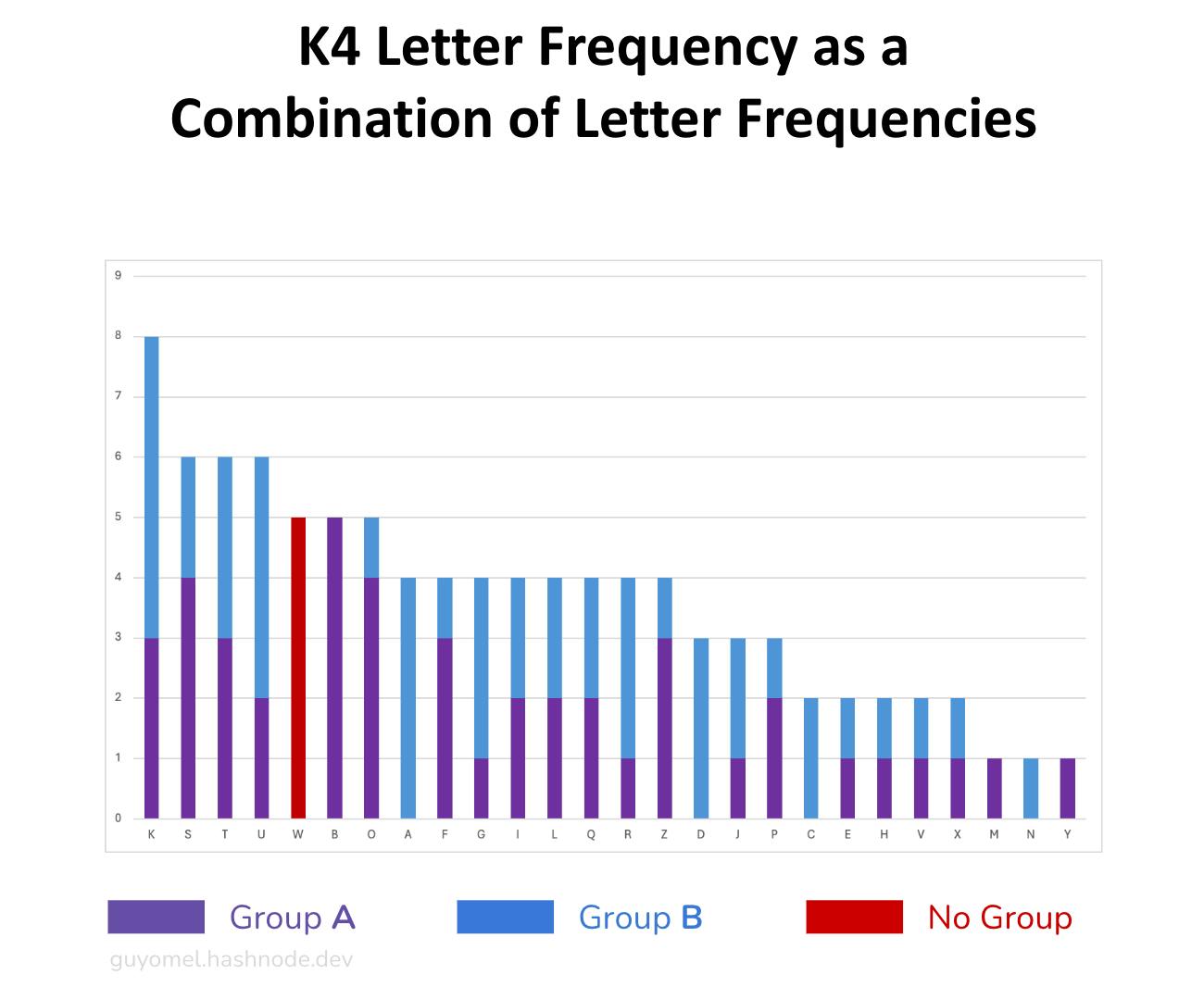
We do not know yet the exact mechanism employed to alter the distributions of K4’s groups. It is, however, important not to assume that identical distribution shapes necessarily mean that the deciphered segments of Group A contain the same letters as the ones of Group B (which would be very unlikely for a natural language). On one hand, this mechanism could have been applied to encrypted segments (second-order encoding). On the other hand, intentional spelling errors, similar to other passages like UNDERGRUUND (K2) or DESPARATLY (K3), could have been introduced to slightly modify the letter frequencies. With this simple technique, one letter’s occurrences are decremented while another’s are incremented. For example, IQLUSION (K1) decrements the Ls while incrementing the Qs. Similarly, superfluous letters could have been introduced in the style of XCANYOUSEEANYTHINGQ (K3).

Illustration: Let’s Encrypt Alice

We can test our hypothesis by applying this technique to a fictitious example.

Let’s say we want to encrypt this passage from Alice’s Adventures in Wonderland:

“You promised to tell me your history, you know,” said Alice.

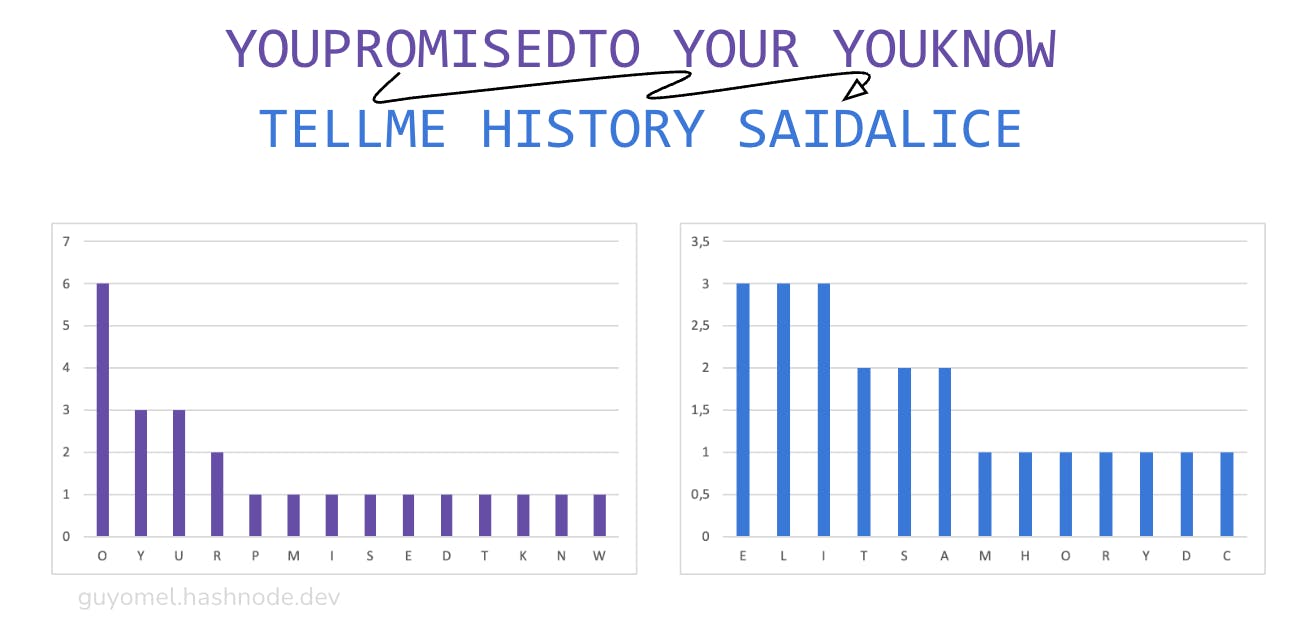
The first step is to transform the sentence by removing the punctuation marks and the spaces and by capitalizing the letters:

Then, the sentence is split in half and segmented, with segments alternated between two groups. Last, the letter frequencies of the respective groups are computed.

The distributions are dissimilar. We want to reduce this difference. To that end, we encode the first group using standard Vigenère (obviously, we could have used a different cipher) and try several keys to improve the situation. The key SECRET quickly emerges as a good candidate (“YOUPROMISEDTO YOUR YOUKNOW” becomes “QSWGVHEMUVHMG CQLV RGYMESP”):

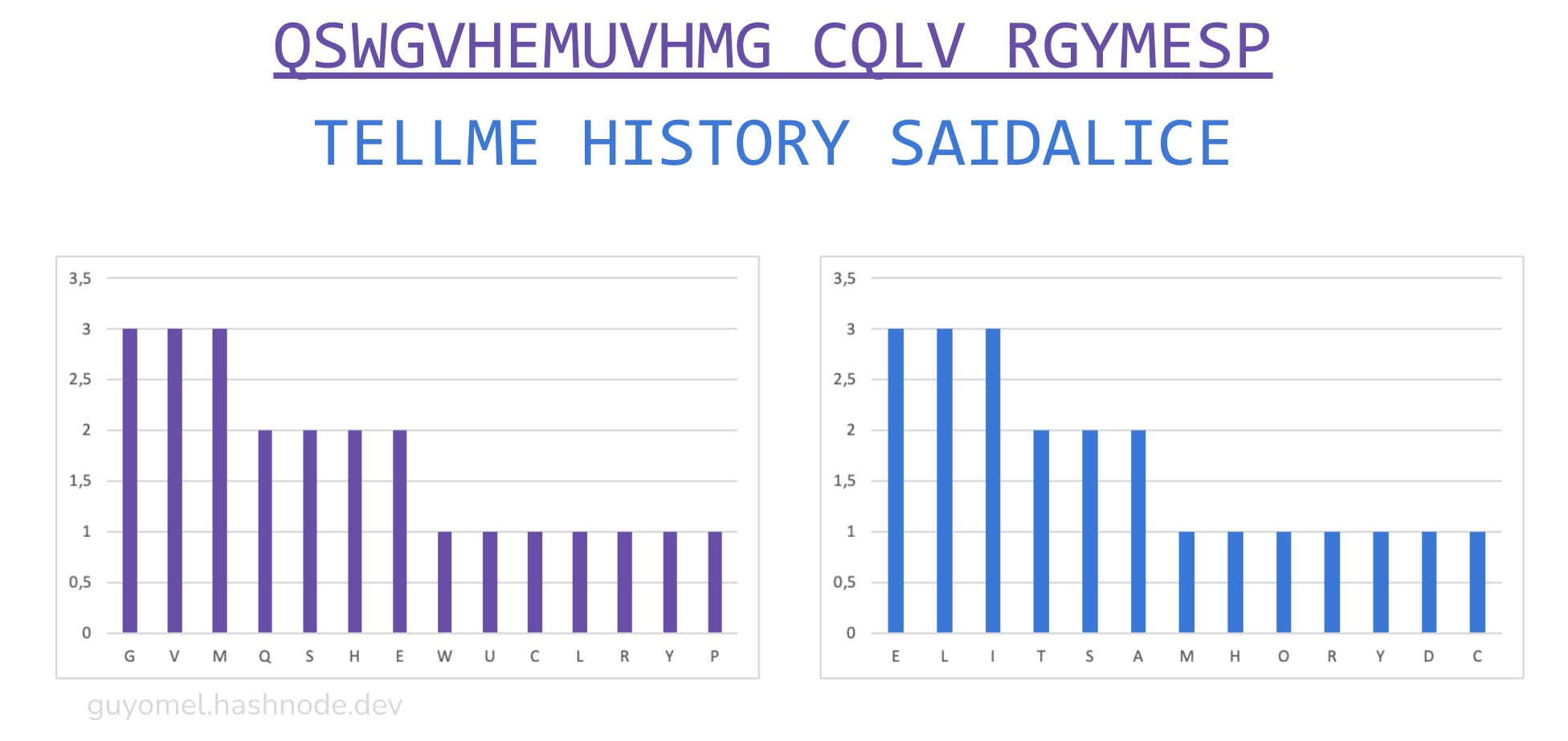
The letter frequency distribution shapes are now similar but have yet to be identical. We need to adjust the second group to make them match. In this case, it is just a matter of adding letters (as the second group is shorter than the first). “TELLME HISTORY SAIDALICE” becomes “YTELLME HISTORY SAIDALICEX”. The original plaintext segments remain intelligible.

We obfuscate the second group for demonstration by merely applying a trivial ROT13 cipher, which preserves the distribution shapes (“YTELLME HISTORY SAIDALICEX” becomes “LGRYYZR UVFGBEL FNVQNYVPRK”).

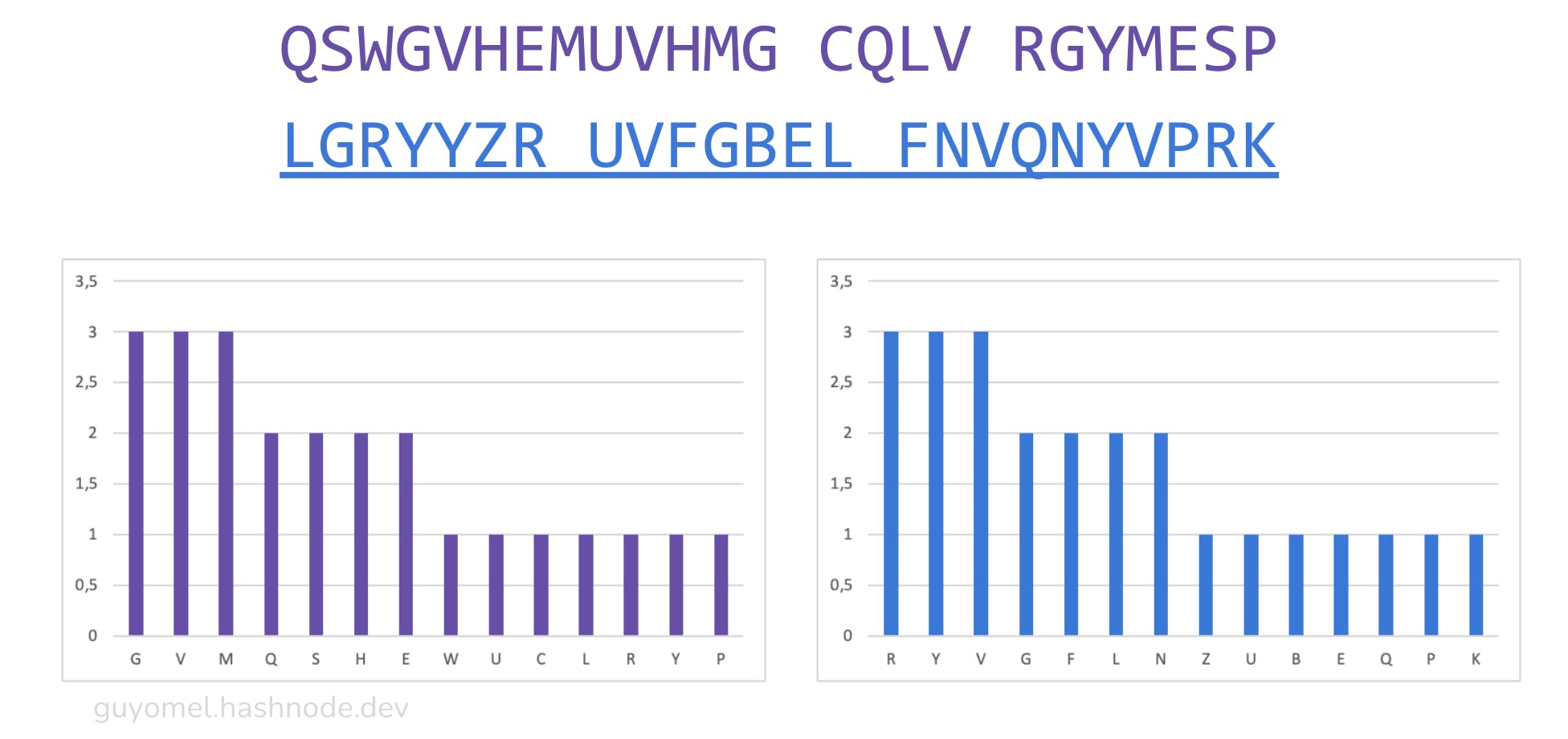
The shapes of the distributions are identical. The last step is to identify a letter not present in the ciphertext segments (‘X’, for instance) and recombine the segments by alternating them:

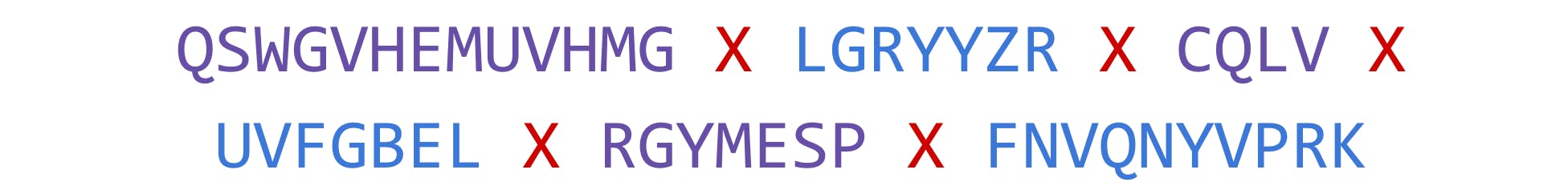
The outcome is a ciphertext that cannot be attacked with classic methods because of the fabricated letter frequency.

Importantly, this example demonstrates that the two plaintext groups are not required to contain the same letters. Also, the separator that combines the segments is one of the most frequent letters in the ciphertext, even though it is the odd one out.

Next Steps

Once the technique is known, the separator is identified, and the correct groups are determined, deciphering this kind of code is a matter of understanding how each group has been “encoded” before attacking it with classic cryptanalysis methods.

This is the path we would like to follow to crack K4.

If (some of) our arguments convince you and you love challenges, do not hesitate to contact us at kryptos@glthr.com. Contributions to K4nundrum are also welcomed.